
Расстояние городских кварталов — метрика, введённая Германом Минковским. Согласно этой метрике, расстояние между двумя точками равно сумме модулей разностей их координат.
У этой метрики много имён. Расстояние городских кварталов также известно как манхэттенское расстояние, метрика прямоугольного города, метрика L1 или норма (см. пространство Lp), метрика городского квартала, метрика такси, метрика Манхэттена, прямоугольная метрика, метрика прямого угла; на её называют метрикой гриды и 4-метрикой[1][2][3].
Название «манхэттенское расстояние» связано с уличной планировкой Манхэттена[4].
Формальное определение
Расстояние городских кварталов между двумя векторами в n-мерном вещественном векторном пространстве с заданной системой координат — сумма длин проекций отрезка между точками на оси координат. Более формально,
где
- и
— векторы.
Например, на плоскости расстояние городских кварталов между и равно
Свойства
Манхэттенское расстояние зависит от вращения системы координат, но не зависит от отражения относительно оси координат или переноса. В геометрии, основанной на манхэттенском расстоянии, выполняются все аксиомы Гильберта, кроме аксиомы о конгруэнтных треугольниках.
Для трёхмерного пространства, шар в этой метрике имеет форму октаэдра, вершины которого лежат на осях координат.
Примеры
| a | b | c | d | e | f | g | h | ||
| 8 | 8 | ||||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
Расстояния в шахматах
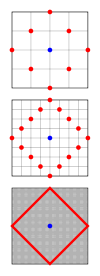
Расстояние между полями шахматной доски для визиря (или ладьи, если расстояние считать в клетках) равно манхэттенскому расстоянию; король пользуется расстоянием Чебышёва , а слон — манхэттенским расстоянием на доске, повёрнутой на 45°.
Пятнашки
Сумма манхэттенских расстояний между костяшками и позициями, в которых они находятся в решённой головоломке «Пятнашки», используется в качестве эвристической функции для поиска оптимального решения[5].
Клеточные автоматы
Множество клеток на двумерном квадратном паркете, манхэттенское расстояние до которых от данной клетки не превышает r, называется окрестностью фон Неймана диапазона (радиуса) r[6].
См. также
Примечания
- ↑ Елена Деза, Мишель Мари Деза. Глава 19. Расстояния на действительной и цифровой плоскостях. 19.1. Метрики на действительной плоскости // Энциклопедический словарь расстояний = Dictionary of Distances. — М: Наука, 2008. — С. 276. — ISBN 978-5-02-036043-3.
- ↑ Кластерный анализ: Меры расстояния
- ↑ Manhattan distance
- ↑ City Block Distance. Spotfire Technology Network.
- ↑ История компьютера: Эвристические функции
- ↑ Weisstein, Eric W. von Neumann Neighborhood (англ.) на сайте Wolfram MathWorld.
Литература
- Eugene F. Krause. Taxicab Geometry. — Dover, 1987. — ISBN 0-486-25202-7.
Ссылки
- city-block metric on PlanetMath
- Weisstein, Eric W. Taxicab Metric (англ.) на сайте Wolfram MathWorld.
- Manhattan distance. Paul E. Black, Dictionary of Algorithms and Data Structures, NIST
- Taxi! - AMS column about Taxicab geometry
- TaxicabGeometry.net - a website dedicated to taxicab geometry research and information
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .










